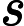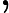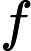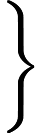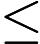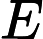最短路徑
術語
- 負邊:權重為負的邊
- 負環:權重和為負的環
- 點源:成為起點的點,分成單源頭及多源頭。
- 鬆弛:單源頭最短路徑中,對於任意兩個點


 ,起點
,起點 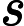 到它們的距離
到它們的距離 



 ,如果
,如果 







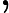
 ,
, 

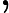
 為邊
為邊 



 的權重,我們可以讓
的權重,我們可以讓 
 更新為
更新為 




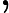
 ,讓
,讓 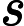 到
到  的距離縮短,這個動作稱為 "鬆弛"。
的距離縮短,這個動作稱為 "鬆弛"。
Floyd-Warshall Algorithm
為多源頭最短路徑,求出所有點對的最短路徑。
Floyd-Warshall 是一種動態規劃問題,以下是他的 dp 式。
時/空間複雜度皆為 



 ,利用滾動陣列技巧,空間複雜度可優化至
,利用滾動陣列技巧,空間複雜度可優化至 




| for (k = 0; k < n; k++)
for (i = 0; i < n; i++)
for (j = 0; j < n; j++)
w[i][j] = w[j][i] = min(w[i][j], w[i][k] + w[k][j]);
|
執行的時候如果 







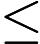
 ,代表存在負環,Floyd-Warshall 是可以判斷負環。
,代表存在負環,Floyd-Warshall 是可以判斷負環。
單點源最短路徑
求出一個點到所有點的最短路徑,其實就是以起點為根,最短路徑是由父節點鬆弛而來的最短路徑樹。我們找最短路徑,就是一直把鬆弛,直到所有點都不能鬆弛,所有點都獲得最短路徑了。要蓋出最短路徑樹,就只要把點指向最後一次被誰鬆弛就好了。
Bellman-Ford Algorithm
為單點源最短路徑,設起點的最短路徑為 0,其他點為無限大,每次對所有邊枚舉,因為最短路徑不會經過同樣的邊第二次,所以只要執行 

 輪,複雜度為
輪,複雜度為 


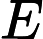
 。如果執行第
。如果執行第  次時還有邊可以鬆弛,代表有負環,Bellman-Ford 也可以當成負環的判斷方法。
次時還有邊可以鬆弛,代表有負環,Bellman-Ford 也可以當成負環的判斷方法。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31 | void bellman_ford(int s)
{
d[s] = 0;
p[s] = s;
for (int i = 0; i < V - 1; i++)
{
for (int ss = 0; ss < V; ss++)
{
for (auto tt : v[ss])
{
if (d[ss] + w[ss][tt] < d[tt])
{
d[tt] = d[ss] + w[ss][tt];
p[tt] = ss;
}
}
}
}
}
bool has_negative_cycle()
{
for (int i = 0; i < V; i++)
{
for (int j = 0; j < V; j++)
{
if (d[i] + w[i][j] < d[j])
return true;
}
}
return false;
}
|
此演算法還有一個優化版本叫做 Shortest Path Faster Algorithm (SPFA),他的做法是枚舉起點是鬆弛過的邊,以鬆弛過的點除非被重新鬆弛,否則不會更動。預期複雜度為 



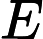
 ,不過最差狀況仍為
,不過最差狀況仍為 


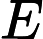
 。
。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38 | struct Edge
{
int t;
long long w;
Edge(){};
Edge(int _t, long long _w) : t(_t), w(_w) {}
};
bool SPFA(int st)
{
vector<int> cnt(n, 0);
bitset<MXV> inq(0);
queue<int> q;
q.push(st);
dis[st] = 0;
inq[st] = true;
while (!q.empty())
{
int cur = q.front();
q.pop();
inq[cur] = false;
for (auto &e : G[cur])
{
if (dis[e.t] <= dis[cur] + e.w)
continue;
dis[e.t] = dis[cur] + e.w;
if (inq[e.t])
continue;
++cnt[e.t];
if (cnt[e.t] > n)
return false; // negtive cycle
inq[e.t] = true;
q.push(e.t);
}
}
return true;
}
|
Dijkstra’s Algorithm
同樣為單點源最短路徑,他的想法和 Prim's Algorithm 類似,每次把離樹根最近的點加入最短路徑樹裡,並把所有與該點相連的邊鬆弛,已經加入的點不會在被鬆弛。
使用 priority_queue 的複雜度為 




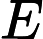

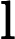


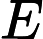
 ,使用費波那契堆,複雜度為
,使用費波那契堆,複雜度為 

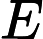






1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51 | struct edge
{
int s, t;
LL d;
edge(){};
edge(int s, int t, LL d) : s(s), t(t), d(d) {}
};
struct heap
{
LL d;
int p; // point
heap(){};
heap(LL d, int p) : d(d), p(p) {}
bool operator<(const heap &b) const { return d > b.d; }
};
int d[N], p[N];
vector<edge> edges;
vector<int> G[N];
bitset<N> vis;
void dijkstra(int ss)
{
priority_queue<heap> Q;
for (int i = 0; i < V; i++)
d[i] = INF;
d[ss] = 0;
p[ss] = -1;
vis.reset() : Q.push(heap(0, ss));
heap x;
while (!Q.empty())
{
x = Q.top();
Q.pop();
int p = x.p;
if (vis[p])
continue;
vis[p] = 1;
for (int i = 0; i < G[p].size(); i++)
{
edge &e = edges[G[p][i]];
if (d[e.t] > d[p] + e.d)
{
d[e.t] = d[p] + e.d;
p[e.t] = G[p][i];
Q.push(heap(d[e.t], e.t));
}
}
}
}
|
而 Dijkstra’s Algorithm 不能處理負邊,原因是一旦點加入最短路徑樹,就不會再被更新,以維持良好複雜度,負邊會破壞此規則。
整理
例題練習